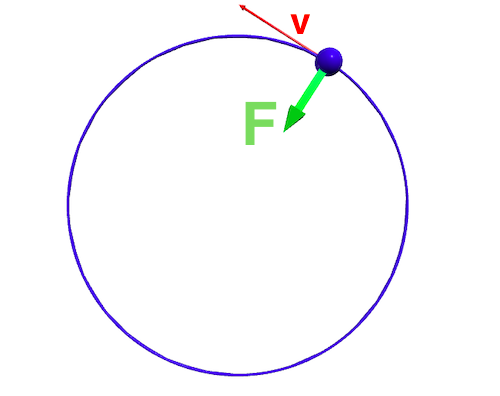
VPython的第五堂課:等速率圓週運動
Lesson5
類別:程式設計
此單元我們要繪製等速率圓週運動的動畫,關於等速率圓週運動,可先參考下圖中於高二物理學習到的相關物理量,或另外再作相關的複習,可幫助對接下來的程式撰寫較有幫助。
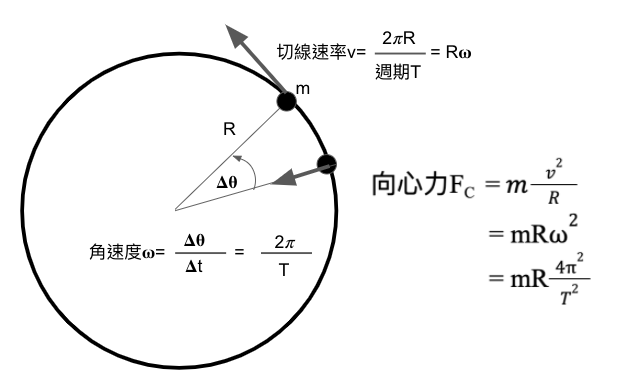
一、等速率圓周運動
我們要利用圓的參數式的想法來繪製運動,若圓周運動的角速度為ω,
且球由正右方開始作逆時鐘的圓周運動,球的x、y座標和時間的關係為下:
x=Rcosθ=Rcos(ωt)
y=Rsinθ=Rsin(ωt)
程式碼無法打出ω和θ,
因此我們自定變數omega取代ω,定變數theta取代θ。
另外,程式中的pi即為π,這是程式預設的變數。
程式碼撰寫如下:
Web VPython 3.2
size=0.8
theta=0
R=10
omega=2*pi
t=0
scene=canvas(width=800, height=600,center=vector(0,0,0), background=color.white)
ball=sphere(pos=vector(R,0,0),radius=size,color=color.blue,make_trail=True)
dt=0.001
while True:
rate(1/dt)
t=t+dt
theta=theta+omega*dt
ball.pos=R*vector(cos(theta),sin(theta),0)
練習1:改變theta一開始的值為pi/6、pi/4、pi/2,看模擬動畫有何不同。
練習2:將上述圓周運動轉動一圈的時間調整和秒針針尖一樣為60秒。
二、加上切線速度的向量
切線速度是一個向量,它的大小v=Rω,方向是圓的切線方向。
此向量的位置和大小設定不難,和上個單元的做法差不多,但向量的方向就比較困難。
由速度的定義可知,一段時間的平均速度方向和位移Δx方向相同,因此我們用位移Δx方向來當作速度的方向。
程式以變數dx表示位移Δx,
並新增一速度向量v_arrow
而位移Δx是末位置-初位置,
在while內利用newpos-prepos算出位移
因此程式碼撰寫如下:
Web VPython 3.2
size=0.8
theta=0
R=10
omega=2*pi
t=0
scene=canvas(width=800, height=600,center=vector(0,0,0), background=color.white)
ball=sphere(pos=vector(R,0,0),radius=size,color=color.blue,make_trail=True)
dx=(0,0,0)
v_arrow=arrow(color=color.red, shaftwidth=0.1)
dt=0.001
while True:
prepos=ball.pos
rate(1/dt)
t=t+dt
theta=theta+omega*dt
ball.pos=R*vector(cos(theta),sin(theta),0)
newpos=ball.pos
dx=newpos-prepos
v_arrow.pos=ball.pos
v_arrow.axis=dx
但執行程式時,會發現沒看到速度的向量,原因是因為我們用速度是用位移的方向,但大小是位移的大小,因位移太小,因此這個動畫無法顯示出來
為了解決此問量,我們可以用位移向量的單位向量的再乘上速度的大小,來得到速度的向量。
取單位向量的作法為vector.norm(),而切線速度的大小v=R*ω,
所以原程式中最後一行的v_arrow要修改如下:
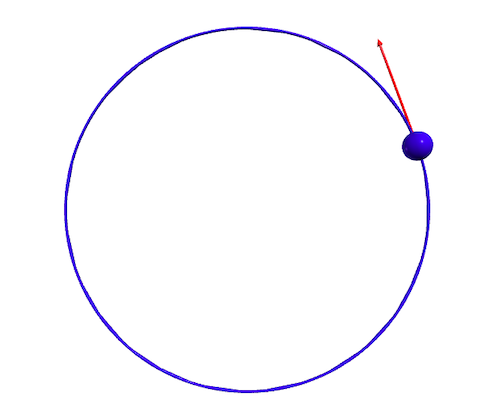
可再乘一個數值使動畫中的v有較適當的大小,如下圖。
課程任務10:在圓周運動上,再加上向心力的向量。