VPython的第六堂課:簡諧運動與單擺
Lesson 6
類別:程式設計
一、簡諧運動
在高二物理簡諧運動的單元,我們學到若將一質量為m的物體連接在一條彈力係數為k的彈簧,且彈簧另一端連接在牆壁上,如下圖,此時若將物體右拉一段距離R再由靜止釋放,則此物體會作振幅為R的簡諧運動(simple harmonic motion, S.H.M.),且其運動恰為等速率圓週運動的投影結果。
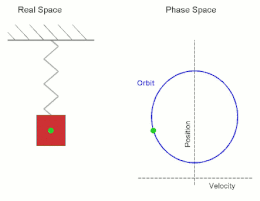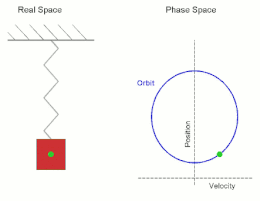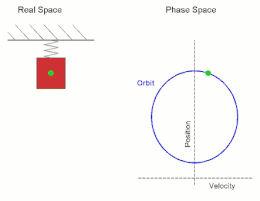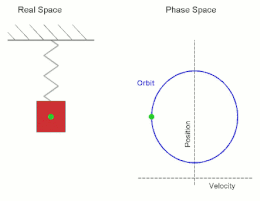
(from 維基百科)
且我們可知物體受力與加速度的關係為:
F = -kx = ma
其中x為彈簧的形變量(伸長or壓縮的大小)
而我們證明若物體拉至右拉一段距離R再靜止釋放,其運動的位置x、速度v和加速度a和時間的關係式如下:
x = Rcos(ωt)
v = -Rωsin(ωt)
a = -Rω²cos(ωt)
其中ω為簡諧運動的角頻率,其大小和物體質量m和彈簧的彈力係數k有關,關係式如下:
ω = √k/m
且簡諧運動的週期T=2π√m/k
1、繪製物件
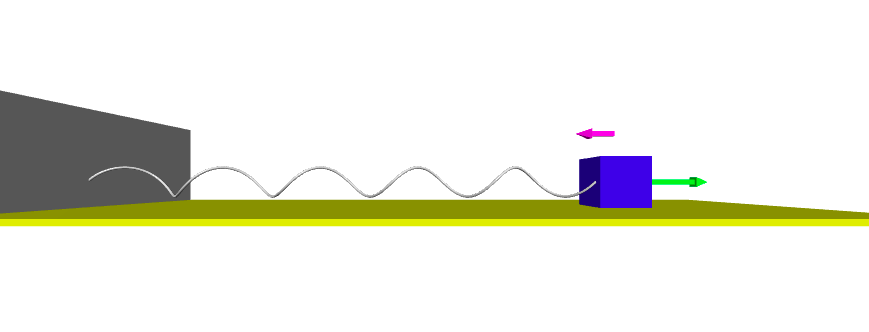
我們先繪製簡諧運動的動畫所需物件,包含牆、物體、地板及彈簧,並設定相關參數,
其中,物體的大小設為size,且其作簡諧運動的振幅為R,因此讓彈簧原長L0的大小設定為R+size*2,讓彈簧原長確定夠長。
並為了讓物體運動的畫面在中間,因此連接彈簧的牆的位置(x方向)設定在-L0處。
假設物體一開始是先拉至最右邊振幅R處靜止釋放,但物體本身大小為size,因此物體初始位置(x方向)設定為R+size/2。
另外,為了讓物體在動畫的中間,也將地板的位置(y方向)設定在-(size+0.1)/2。
而彈簧我們是以helix(螺旋線)來畫出其樣子。
程式碼如下:
Web VPython 3.2
#木塊質量 4 kg
m= 4
# 木塊邊長 1 m
size = 1
# 振幅 5 m
R = 5
# 彈性常數 1 N/m
k = 1
# 彈簧原長
L0 = R + size*2
#場景scene設定
scene = canvas(title = "Simple Harmonic Motion", width = 900, height = 400, x = 0, y = 0, background = vector(1, 1, 1))
#牆wall
wall = box(pos = vector(-L0, size-(size+0.1)/2, 0), length = 0.1, height = size*2, width = R, color = vector(0.9, 0.9, 0.9))
#物體object
object = box(pos = vector(R+size/2, 0, 0), length = size, height = size, width = size, color = color.blue)
#地板floor
floor = box(pos = vector(0, -(size+0.1)/2, 0), length = 2*L0, height = 0.1, width = R, color = color.yellow)
#彈簧spring
spring = helix(pos = vector(-L0, 0, 0), radius = 0.3*size, thickness = 0.05*size, color = vector(0.9, 0.9, 0.9))
spring.axis = object.pos - spring.pos - vector(size/2, 0, 0)
繪製結果如下圖所示

2、使物體作簡諧運動
我們可利用彈力F=-kx=ma,求出物體的加速度a,
再利用之前繪製等加速度的方法由加速度求速度v再求位置x,
以畫出此物體作簡諧運動的樣子,請於上述程式碼後,再加上下方程式,程式碼如下:
object.v= vector(0,0,0)
# 時間
t = 0
# 時間間隔
dt = 0.001
while(True):
rate(1000)
# 計算彈簧長度、伸長量、回復力
spring.axis = object.pos - spring.pos - vector(size/2, 0, 0)
F = -k * (spring.axis - vector(L0, 0, 0))
# 計算木塊加速度, 更新速度、位置
object.a = F/m
object.v = object.v+object.a*dt
object.pos =object.pos+object.v*dt
完成動畫如下
課程任務11:請觀察此簡諧運動的週期T,其大小是否和公式T=2π√m/k的結果相同,並嘗試更改動畫中物體的質量m和彈簧的彈力係數k,並再次觀察動畫的週期和公式算出來的值是否相同。
課程任務12:任務11中的週期,除了直接觀察測量外,試著透過程式的修改,直接從動畫中得到簡諧運動的週期大小。
提示:週期為物體剛成一次循環回到原位置所需的時間。
課程任務13:請畫上物體作簡諧運動時的速度向量和加速度向量
單擺
1、繪製物件
Web VPython 3.2
# 小球半徑
size = 0.2
# 小球質量
m = 1
# 擺長
L = 5
# 起始擺角, 用 radians 將單位換成 rad
theta0 = radians(30)
# 擺角
theta = theta0
# 重力加速度
g = 9.8
# 單擺週期理論值, L = 5, g = 9.8, T = 4.48798950512828
T = 2*pi*sqrt(L/g)
# 角加速度, 初始值為 0
alpha = 0
# 角速度, 初始值為 0
omega = 0
scene = canvas(title = "Pendulum", width = 700, height = 600, x = 0, y = 0, background = vector(1, 1, 1))
ceiling = box(pos = vector(0, L/2 + 0.05, 0), length = L, height = 0.1, width = L/2, color = color.blue)
ball = sphere(pos = vector(L*sin(theta0), L/2 - L*cos(theta0), 0), radius = size, color = color.red, make_trail = True, retain = 100)
rope = cylinder(pos = vector(0, L/2, 0), axis = ball.pos - vector(0, L/2, 0), radius = 0.1*size, color = color.yellow)
2、使單擺開始擺動
t = 0
# 時間間隔
dt = 0.001
while(True):
rate(1000)
# 計算小球所受力矩、角加速度、角速度、擺角
r = ball.pos - vector(0, L/2, 0)
alpha = -m*g*ball.pos.x/(m*L*L)
omega = omega+ alpha*dt
theta = theta+omega*dt
# 更新小球的位置、速度, 繩子的軸方向及長度
ball.pos = vector(L*sin(theta), L/2 - L*cos(theta), 0)
rope.axis = r
t =t+ dt
完成動畫如下